| In the year 598 a great mathematician was born by the name of Brahmagupta. He wrote two early works on mathematics and astronomy called the Brahmasphutasiddhanta and the Khandakhadyaka. Besides these titles being quite a mouthful, these works had great mathematical value. It was Brahmagupta who first gave the rules to compute with zero in the Brahmasphutasiddhanta. Interestingly Brahmagupta explained negative numbers as debts and positive numbers as fortunes. In class we looked at these properties of zero that Brahmagupta discovered. We agreed with most of the basic ideas such as a negative number minus zero is a negative number, and the same for a positive number. And that the product of zero multiplied by zero or a negative or positive number is zero. However there were two properties that questioned. |
One property was "Positive or negative numbers when divided by zero is a fraction the zero as a denominator." As we discussed this property as a class we immediately agreed that a number divided by zero is undefined and cannot simply be written as a fraction. In the modern math world we do not accept dividing by zero.
This, however, led us to another questionable property. Brahmagupta said that "zero divided by zero is zero." At first I wanted to agree to this and it led to an interesting discussion. After talking about this as a group, I eventually came to the conclusion that zero divided by zero must be undefined because you can divide something by 0 as many times as you want and it will stay the same.
After talking about these properties of zero and positive and negative numbers Professor Golden brought up the common question: why is a negative times a negative a positive number? This proved to be a very challenging question to answer, and although Brahmagupta wrote it down as a property, he did not explain why. Our class began racking our brains to explain this phenomenon.
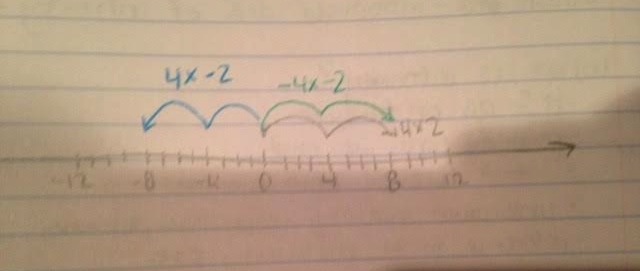
The explanation that made the most sense to me used a number line. My colleagues pointed out that multiplication is like jumping along a number line. A negative changes the direction, so a positive times a negative will cause jumping in the negative direction. A negative times a negative will then change the direction again to cause jumping in the positive direction. This can be seen below with 4 times 2. Positive 4 times positive 2 is represented by the pencil in the positive direction. Positive 4 times a negative 2 is blue ink in the negative direction and negative 4 times negative 2 is the green ink in the positive direction. As you can see the negative signs are what change the direction on the number line.
This, however, led us to another questionable property. Brahmagupta said that "zero divided by zero is zero." At first I wanted to agree to this and it led to an interesting discussion. After talking about this as a group, I eventually came to the conclusion that zero divided by zero must be undefined because you can divide something by 0 as many times as you want and it will stay the same.
After talking about these properties of zero and positive and negative numbers Professor Golden brought up the common question: why is a negative times a negative a positive number? This proved to be a very challenging question to answer, and although Brahmagupta wrote it down as a property, he did not explain why. Our class began racking our brains to explain this phenomenon.
The explanation that made the most sense to me used a number line. My colleagues pointed out that multiplication is like jumping along a number line. A negative changes the direction, so a positive times a negative will cause jumping in the negative direction. A negative times a negative will then change the direction again to cause jumping in the positive direction. This can be seen below with 4 times 2. Positive 4 times positive 2 is represented by the pencil in the positive direction. Positive 4 times a negative 2 is blue ink in the negative direction and negative 4 times negative 2 is the green ink in the positive direction. As you can see the negative signs are what change the direction on the number line.
| Professor Golden also explained another reason why a negative times a negative is a positive using multiple chains. Using a multiple chain of -2 we can see that decreasing a multiplier of -2 by 1 increases the product by 2 each time. This consistently occurs so we know that as we move from a positive multiplier to a negative multiplier we will move to positive products as seen to the left. This reasoning is easy to understand. I like that Professor Golden used the consistency of math so that this explanation cannot be questioned. |
Brahmagupta clearly made mathematical advances that were important in his day, but I am glad that we have come a long way with understanding zero since then. Hooray for modern mathematics!

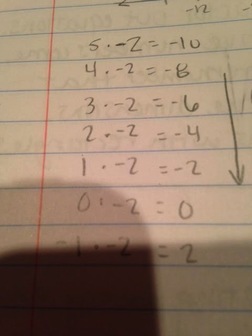




 RSS Feed
RSS Feed
